Slični zadaci
A positive integer  is called balanced, if
is called balanced, if 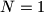 or if
or if  can be written as a product of an even number of not necessarily distinct primes. Given positive integers
can be written as a product of an even number of not necessarily distinct primes. Given positive integers  and
and  , consider the polynomial
, consider the polynomial  defined by
defined by 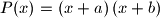 .
.
a) Prove that there exist distinct positive integers and
and  such that all the number
such that all the number 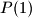 ,
, 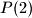 , ...,
, ..., 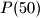 are balanced.
are balanced.
b) Prove that if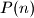 is balanced for all positive integers
is balanced for all positive integers  , then
, then 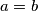 .
.
Proposed by Jorge Tipe, Peru
 is called balanced, if
is called balanced, if 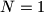 or if
or if  can be written as a product of an even number of not necessarily distinct primes. Given positive integers
can be written as a product of an even number of not necessarily distinct primes. Given positive integers  and
and  , consider the polynomial
, consider the polynomial  defined by
defined by 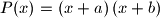 .
.a) Prove that there exist distinct positive integers
 and
and  such that all the number
such that all the number 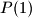 ,
, 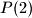 , ...,
, ..., 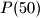 are balanced.
are balanced.b) Prove that if
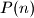 is balanced for all positive integers
is balanced for all positive integers  , then
, then 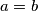 .
.Proposed by Jorge Tipe, Peru
 Školjka
Školjka 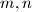 takve da vrijedi:
takve da vrijedi: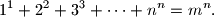
 ,
,  ,
,  ,
,  be distinct positive integers,
be distinct positive integers, 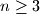 . Prove that there exist distinct indices
. Prove that there exist distinct indices  and
and  such that
such that 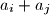 does not divide any of the numbers
does not divide any of the numbers 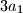 ,
, 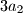 ,
, 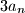 .
. 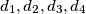 vrijedi:
vrijedi: 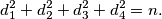
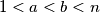 , the number
, the number 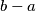 divides
divides  i
i  za koje vrijedi
za koje vrijedi 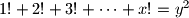 .
.