Dani su brojevi
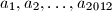
iz intervala
![\left[0,1\right]](/media/m/e/7/f/e7f4d22d3ff05cc9bd2c7aa876c2715c.png)
. Dokaži nejednakost:
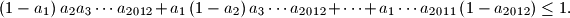
%V0
Dani su brojevi $a_1, a_2, \ldots, a_{2012}$ iz intervala $\left[0,1\right]$. Dokaži nejednakost:
$$ \left(1-a_1\right)a_2a_3\cdots a_{2012} + a_1\left(1-a_2\right)a_3 \cdots a_{2012} + \cdots + a_1\cdots a_{2011}\left(1-a_{2012}\right) \leq 1 \text{.}$$