Šest otoka povezano je linijama jednog trajektnog i jednog hidrogliserskog poduzeća. Svaka dva otoka povezana su (u oba smjera) linijom točno jednog od ova dva poduzeća. Dokaži da je moguće ciklički posjetiti četiri otoka koristeći linije samo jednog poduzeća (tj. da postoje četiri otoka 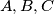 i
i  i poduzeće čiji brodovi plove na linijama
i poduzeće čiji brodovi plove na linijama 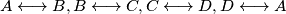 ).
).
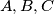 i
i  i poduzeće čiji brodovi plove na linijama
i poduzeće čiji brodovi plove na linijama 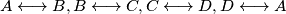 ).
). Slični zadaci
Konačan broj polja beskonačne kvadratne mreže obojan je crnom bojom. Dokažite da je u toj ravnini moguće odabrati konačno mnogo kvadrata koji zadovoljavaju svaki od sljedećih uvjeta:
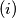 Unutrašnjosti svaka dva različita kvadrata su disjunktne (imaju prazan presjek).
Unutrašnjosti svaka dva različita kvadrata su disjunktne (imaju prazan presjek).
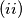 Svako crno obojeno polje leži u nekom od tih kvadrata.
Svako crno obojeno polje leži u nekom od tih kvadrata.
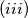 Površina crnih polja u svakom od odabranih kvadrata je barem
Površina crnih polja u svakom od odabranih kvadrata je barem  , a najvise
, a najvise  površine tog kvadrata.
površine tog kvadrata.
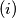 Unutrašnjosti svaka dva različita kvadrata su disjunktne (imaju prazan presjek).
Unutrašnjosti svaka dva različita kvadrata su disjunktne (imaju prazan presjek).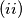 Svako crno obojeno polje leži u nekom od tih kvadrata.
Svako crno obojeno polje leži u nekom od tih kvadrata.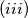 Površina crnih polja u svakom od odabranih kvadrata je barem
Površina crnih polja u svakom od odabranih kvadrata je barem  , a najvise
, a najvise  površine tog kvadrata.
površine tog kvadrata. Na otoku živi  domorodaca. Svaka dva su ili prijatelji ili neprijatelji. Jednog dana poglavica naredi svim stanovnicima (uključujući i sebe) da si naprave i da nose kamene ogrlice, tako da svaka dva prijatelja imaju barem po jedan istovrsni kamen u svojim ogrlicama, a da se sva kamenja u ogrlicama dvaju neprijatelja razlikuju. (Ogrlica može biti i bez kamenja) Dokažite da se poglavičina zapovijed može izvršiti koristeći
domorodaca. Svaka dva su ili prijatelji ili neprijatelji. Jednog dana poglavica naredi svim stanovnicima (uključujući i sebe) da si naprave i da nose kamene ogrlice, tako da svaka dva prijatelja imaju barem po jedan istovrsni kamen u svojim ogrlicama, a da se sva kamenja u ogrlicama dvaju neprijatelja razlikuju. (Ogrlica može biti i bez kamenja) Dokažite da se poglavičina zapovijed može izvršiti koristeći  različitih vrsta kamenja, i da se općenito ovo ne može postići s manje kamenja.
različitih vrsta kamenja, i da se općenito ovo ne može postići s manje kamenja.
 domorodaca. Svaka dva su ili prijatelji ili neprijatelji. Jednog dana poglavica naredi svim stanovnicima (uključujući i sebe) da si naprave i da nose kamene ogrlice, tako da svaka dva prijatelja imaju barem po jedan istovrsni kamen u svojim ogrlicama, a da se sva kamenja u ogrlicama dvaju neprijatelja razlikuju. (Ogrlica može biti i bez kamenja) Dokažite da se poglavičina zapovijed može izvršiti koristeći
domorodaca. Svaka dva su ili prijatelji ili neprijatelji. Jednog dana poglavica naredi svim stanovnicima (uključujući i sebe) da si naprave i da nose kamene ogrlice, tako da svaka dva prijatelja imaju barem po jedan istovrsni kamen u svojim ogrlicama, a da se sva kamenja u ogrlicama dvaju neprijatelja razlikuju. (Ogrlica može biti i bez kamenja) Dokažite da se poglavičina zapovijed može izvršiti koristeći  različitih vrsta kamenja, i da se općenito ovo ne može postići s manje kamenja.
različitih vrsta kamenja, i da se općenito ovo ne može postići s manje kamenja. Na nekom turističkom putovanju bilo je ukupno  turista. Utvrđeno je da su bilo koja dvojica od njih bili međusobno "na ti" ili "na vi" ili uopće nisu razgovarali. Dokažite da među tih
turista. Utvrđeno je da su bilo koja dvojica od njih bili međusobno "na ti" ili "na vi" ili uopće nisu razgovarali. Dokažite da među tih  ljudi postoje bar trojica koji su međusobno bili "na ti" ili bar trojica koji su međusobno bili "na vi" ili bar trojica koji međusobno nisu razgovarali.
ljudi postoje bar trojica koji su međusobno bili "na ti" ili bar trojica koji su međusobno bili "na vi" ili bar trojica koji međusobno nisu razgovarali.
 turista. Utvrđeno je da su bilo koja dvojica od njih bili međusobno "na ti" ili "na vi" ili uopće nisu razgovarali. Dokažite da među tih
turista. Utvrđeno je da su bilo koja dvojica od njih bili međusobno "na ti" ili "na vi" ili uopće nisu razgovarali. Dokažite da među tih  ljudi postoje bar trojica koji su međusobno bili "na ti" ili bar trojica koji su međusobno bili "na vi" ili bar trojica koji međusobno nisu razgovarali.
ljudi postoje bar trojica koji su međusobno bili "na ti" ili bar trojica koji su međusobno bili "na vi" ili bar trojica koji međusobno nisu razgovarali.  Školjka
Školjka 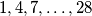 (razlika dvaju uzastopnih je
(razlika dvaju uzastopnih je  ) raspoređeno je u krug. Sa
) raspoređeno je u krug. Sa  označimo najveću od deset suma koje dobivamo tako da svaki od brojeva zbrojimo s dva njemu susjedna broja. Koja je najmanja vrijednost broja
označimo najveću od deset suma koje dobivamo tako da svaki od brojeva zbrojimo s dva njemu susjedna broja. Koja je najmanja vrijednost broja  kockica duljine brida
kockica duljine brida  čije su
čije su 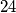 strane obojane crveno, a preostalih
strane obojane crveno, a preostalih 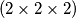 na čijem oplošju će biti jednak broj crvenih i plavih kvadrata
na čijem oplošju će biti jednak broj crvenih i plavih kvadrata 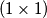 .
. 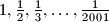 . Učenik odabire dva broja s ploče, recimo
. Učenik odabire dva broja s ploče, recimo  i
i  , te izračuna broj
, te izračuna broj 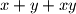 , rezultat zapiše na ploču, a
, rezultat zapiše na ploču, a 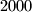 puta.
puta.