Let

be an acute triangle with circumcircle

. Let
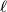
be a tangent line to

, and let
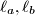
and
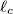
be the lines obtained by reflecting
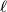
in the lines

,

and

, respectively. Show that the circumcircle of the triangle determined by the lines
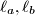
and
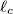
is tangent to the circle

.
Proposed by Japan
%V0
Let $ABC$ be an acute triangle with circumcircle $\Gamma$. Let $\ell$ be a tangent line to $\Gamma$, and let $\ell_a, \ell_b$ and $\ell_c$ be the lines obtained by reflecting $\ell$ in the lines $BC$, $CA$ and $AB$, respectively. Show that the circumcircle of the triangle determined by the lines $\ell_a, \ell_b$ and $\ell_c$ is tangent to the circle $\Gamma$.
Proposed by Japan