Neka su
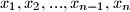
pozitivni realni brojevi takvi da je
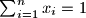
. Dokaži nejednakost
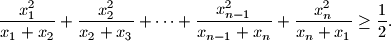
%V0
Neka su $x_1, x_2, . . . , x_{n-1}, x_n$ pozitivni realni brojevi takvi da je $\sum_{i=1}^{n}x_i = 1$. Dokaži nejednakost
$$\frac{x_1^2}{x_1+x_2} + \frac{x_2^2}{x_2+x_3} + \cdots + \frac{x_{n-1}^2}{x_{n-1}+x_n} + \frac{x_n^2}{x_n+x_1} \geq \frac{1}{2}.$$