Dan je šesterokut
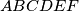
čije se dijagonale
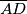
,
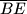
i
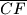
sijeku u
jednoj točki koja je ujedno polovište svake od tih dijagonala.
Dokaži da je površina danog šesterokuta dvostruko veća od površine trokuta
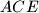
.
%V0
Dan je šesterokut $ABCDEF$ čije se dijagonale $\overline{AD}$, $\overline{BE}$ i $\overline{CF}$ sijeku u
jednoj točki koja je ujedno polovište svake od tih dijagonala.
Dokaži da je površina danog šesterokuta dvostruko veća od površine trokuta $ACE$.