Dan je trapez

kojem su kutovi uz osnovicu

šiljasti, a dijagonale su mu međusobno okomite i sijeku se u točki

. Polupravac
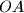
siječe kružnicu s promjerom

u točki

, a polupravac
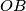
siječe kružnicu s promjerom

u točki

.
Dokaži da točke

,

,

i

leže na jednoj kružnici.
%V0
Dan je trapez $ABCD$ kojem su kutovi uz osnovicu $\overline{AB}$ šiljasti, a dijagonale su mu međusobno okomite i sijeku se u točki $O$. Polupravac $OA$ siječe kružnicu s promjerom $\overline{BD}$ u točki $M$, a polupravac $OB$ siječe kružnicu s promjerom $\overline{AC}$ u točki $N$.
Dokaži da točke $M$, $N$, $C$ i $D$ leže na jednoj kružnici.