Neka je

šiljastokutni trokut i

njegov ortocentar. Pravac kroz točku

okomit na

i pravac kroz točku

okomit na

sijeku se u točki

. Kružnica sa središtem u točki

koja prolazi točkom

siječe kružnicu opisanu trokutu

u točkama

i

.
Dokaži da vrijedi
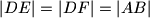
.
%V0
Neka je $ABC$ šiljastokutni trokut i $H$ njegov ortocentar. Pravac kroz točku $A$ okomit na $\overline{AC}$ i pravac kroz točku $B$ okomit na $\overline{BC}$ sijeku se u točki $D$. Kružnica sa središtem u točki $C$ koja prolazi točkom $H$ siječe kružnicu opisanu trokutu $ABC$ u točkama $E$ i $F$.
Dokaži da vrijedi $|DE|=|DF|=|AB|$.