1 - Indukcija Uvod
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Matematička indukcija je metoda dokazivanja koja se najčešće koristi kada želimo dokazati da neka tvrdnja vrijedi za sve prirodne brojeve. Sastoji od tri dijela, baze, u kojoj dokazujemo tvrdnju za neki početni broj, najčešće 1, pretpostavke, u kojoj pretpostavljamo da tvrdnja vrijedi za neki prirodan broj  i koraka u kojemu koristeći pretpostavku pokazujemo da tvrdnja vrijedi i za
i koraka u kojemu koristeći pretpostavku pokazujemo da tvrdnja vrijedi i za  . Na taj način smo dokazali da tvrdnja zaista vrijedi za sve prirodne brojeve. Jednostavan način za vizualizirati indukciju je zamisliti brojeve kao domine. U koraku pokazujemo da, ako padne domina broj
. Na taj način smo dokazali da tvrdnja zaista vrijedi za sve prirodne brojeve. Jednostavan način za vizualizirati indukciju je zamisliti brojeve kao domine. U koraku pokazujemo da, ako padne domina broj  , ona će srušiti dominu
, ona će srušiti dominu  , a u bazi pokazujemo da
, a u bazi pokazujemo da
će prva domina stvarno pasti. Tada smo sigurno da će sve domine pasti.
Primjer jedne jednostavne indukcije:
Dokažimo da je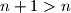 za
za 
Baza

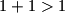
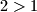
Ova tvrdnja očito vrijedi
Pretpostavka
Pretpostavimo da vrijedi
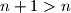
za neki prirodan broj .
.
Korak
Želimo dokazati da
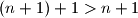 to jest
to jest 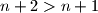
Iz pretpostavke znamo da je
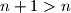 , pa pridodajmo sada na obje strane nejednakosti
, pa pridodajmo sada na obje strane nejednakosti 
dobivamo:
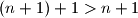
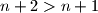
Čime zavrsava korak indukcije
Kako smo pokazali da tvrdnja vrijedi za , i da ako vrijedi za
, i da ako vrijedi za  , vrijedi i za
, vrijedi i za  , očito ta tvrdnja vrijedi za svaki prirodni broj.
, očito ta tvrdnja vrijedi za svaki prirodni broj.
 i koraka u kojemu koristeći pretpostavku pokazujemo da tvrdnja vrijedi i za
i koraka u kojemu koristeći pretpostavku pokazujemo da tvrdnja vrijedi i za  . Na taj način smo dokazali da tvrdnja zaista vrijedi za sve prirodne brojeve. Jednostavan način za vizualizirati indukciju je zamisliti brojeve kao domine. U koraku pokazujemo da, ako padne domina broj
. Na taj način smo dokazali da tvrdnja zaista vrijedi za sve prirodne brojeve. Jednostavan način za vizualizirati indukciju je zamisliti brojeve kao domine. U koraku pokazujemo da, ako padne domina broj  , ona će srušiti dominu
, ona će srušiti dominu  , a u bazi pokazujemo da
, a u bazi pokazujemo da će prva domina stvarno pasti. Tada smo sigurno da će sve domine pasti.
Primjer jedne jednostavne indukcije:
Dokažimo da je
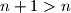 za
za 
Baza

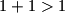
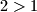
Ova tvrdnja očito vrijedi
Pretpostavka
Pretpostavimo da vrijedi
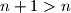
za neki prirodan broj
 .
.Korak
Želimo dokazati da
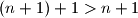 to jest
to jest 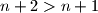
Iz pretpostavke znamo da je
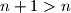 , pa pridodajmo sada na obje strane nejednakosti
, pa pridodajmo sada na obje strane nejednakosti 
dobivamo:
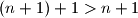
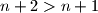
Čime zavrsava korak indukcije
Kako smo pokazali da tvrdnja vrijedi za
 , i da ako vrijedi za
, i da ako vrijedi za  , vrijedi i za
, vrijedi i za  , očito ta tvrdnja vrijedi za svaki prirodni broj.
, očito ta tvrdnja vrijedi za svaki prirodni broj. Izvor: Nepoznato
 Školjka
Školjka 
