1 - Invarijante Uvod
Kvaliteta:
Avg: 5,0Težina:
Avg: 2,5 U nekim se zadacima susrećemo sa sustavom koji se mijenja po određenim pravilima. U takvim je zadacima ćesto korisno potražiti neku veličinu koju ta pravila ne mijenjaju. Takvu veličinu, koju se ne mijenja nikakvom dozvoljenom promjenom sustava, zovemo invarijantp,.
Česti primjeri invarijanti su: ostatak koji suma daje pri djeljenju s za neki prirodni
za neki prirodni  ili, primjerice, njihov umnožak.
ili, primjerice, njihov umnožak.
Primjer zadatka i zapisa rješenja:
Neka su dozvoljeni koraci promjene uređenog para
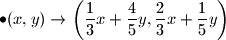
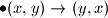
(Dakle, primjenjujući prvi korak na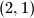 dobivamo
dobivamo 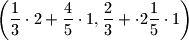 što je jednako
što je jednako 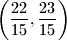 . Sada možemo, na primjer primjeniti drugi dozvoljeni korak i dobiti
. Sada možemo, na primjer primjeniti drugi dozvoljeni korak i dobiti 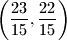 , pa opet možemo primjeniti prvi, i tako dalje.)
, pa opet možemo primjeniti prvi, i tako dalje.)
Pitanje: Možemo li od brojeva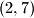 doći do
doći do 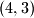 ?
?
Rješenje:
Primjetimo da u oba moguća koraka (promjene) prije i nakon promjene imamo istu sumu uređenog para. To jest primjetimo da:
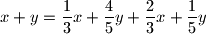
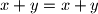
i
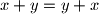
Dakle, što god mi radili, suma uređenog para se neće promijeniti. Suma para od kojeg počinjemo je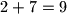 , a moramo doći do
, a moramo doći do 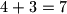 . Kako
. Kako 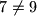 , vidimo da to nije moguće.
, vidimo da to nije moguće.
Česti primjeri invarijanti su: ostatak koji suma daje pri djeljenju s
 za neki prirodni
za neki prirodni  ili, primjerice, njihov umnožak.
ili, primjerice, njihov umnožak.Primjer zadatka i zapisa rješenja:
Neka su dozvoljeni koraci promjene uređenog para

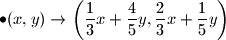
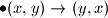
(Dakle, primjenjujući prvi korak na
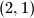 dobivamo
dobivamo 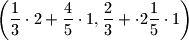 što je jednako
što je jednako 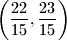 . Sada možemo, na primjer primjeniti drugi dozvoljeni korak i dobiti
. Sada možemo, na primjer primjeniti drugi dozvoljeni korak i dobiti 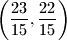 , pa opet možemo primjeniti prvi, i tako dalje.)
, pa opet možemo primjeniti prvi, i tako dalje.)Pitanje: Možemo li od brojeva
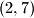 doći do
doći do 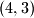 ?
?Rješenje:
Primjetimo da u oba moguća koraka (promjene) prije i nakon promjene imamo istu sumu uređenog para. To jest primjetimo da:
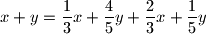
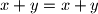
i
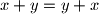
Dakle, što god mi radili, suma uređenog para se neće promijeniti. Suma para od kojeg počinjemo je
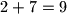 , a moramo doći do
, a moramo doći do 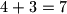 . Kako
. Kako 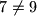 , vidimo da to nije moguće.
, vidimo da to nije moguće. Izvor: Nepoznato
Komentari:
lamijanumber1, 20. siječnja 2016. 16:37
 Školjka
Školjka 
