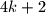
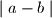
Na ploči su napisani brojevi od do , gdje je prirodan broj. Možemo odabrati neka broja i obrisati oba i umjesto njih napisati . Dokaži da, kako god birali, na kraju će ostati neparan broj.
%V0
Na ploči su napisani brojevi od $1$ do $4k+2$, gdje je $k$ prirodan broj. Možemo odabrati neka $2$ broja i obrisati oba i umjesto njih napisati $\mid a - b \mid$. Dokaži da, kako god birali, na kraju će ostati neparan broj.
Školjka 
do 
, gdje je 
prirodan broj. Možemo odabrati neka 
broja i obrisati oba i umjesto njih napisati 
. Dokaži da, kako god birali, na kraju će ostati neparan broj.