Kamp '13 - Angle Chasing 6.
Dodao/la:
arhiva3. studenoga 2013. Dijagonale tetivnog četverokuta

sijeku se u točki

. Kružnica

opisana trokutu
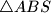
siječe pravac

u točki

, a kružnica

opisana trokutu
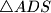
siječe pravac

u točki

. Dokažite da su točke

,

i

kolinearne.
%V0
Dijagonale tetivnog četverokuta $ABCD$ sijeku se u točki $S$. Kružnica $k_1$ opisana trokutu $\triangle ABS$ siječe pravac $BC$ u točki $M$, a kružnica $k_2$ opisana trokutu $\triangle ADS$ siječe pravac $CD$ u točki $N$. Dokažite da su točke $S$, $M$ i $N$ kolinearne.
Izvor: Kamp 2013. - Angle Chasing, L. V.