Kamp '13 - Kombinatorika 5.
Dodao/la:
arhiva3. studenoga 2013. Neka su

i

prirodni brojevi, te
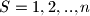
.
a) Odredite ukupan broj svih uređenih

-torki u parovima disjunktnih podskupova od

čija je unija

.
b) Isto kao pod a), samo što podskupovi od

ne moraju biti disjunktni.
%V0
Neka su $n$ i $k$ prirodni brojevi, te $S={1,2,..,n}$.
a) Odredite ukupan broj svih uređenih $k$-torki u parovima disjunktnih podskupova od $S$ čija je unija $S$.
b) Isto kao pod a), samo što podskupovi od $S$ ne moraju biti disjunktni.
Izvor: Kamp 2013. - Kombinatorika, M. M.