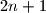
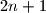
Neka je prirodan broj. Dano je utega cjelobrojne mase u gramima. Koji god uklonili, preostali se mogu grupirati u dvije skupine od po utega, tako da su im mase jednake. Dokažite da svih utega ima jednaku masu.
%V0
Neka je $n$ prirodan broj. Dano je $2n+1$ utega cjelobrojne mase u gramima. Koji god uklonili, preostali se mogu grupirati u dvije skupine od po $n$ utega, tako da su im mase jednake. Dokažite da svih $2n+1$ utega ima jednaku masu.
Školjka 
prirodan broj. Dano je 
utega cjelobrojne mase u gramima. Koji god uklonili, preostali se mogu grupirati u dvije skupine od po