Kamp '13 - Kombinatorika 15.
Dodao/la:
arhiva3. studenoga 2013. Dokaži da bilo koji
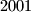
-člani podskup od
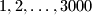
sadrži

elementa od kojih su svaka

međusobno relativno prosta.
%V0
Dokaži da bilo koji $2001$-člani podskup od ${1, 2, \dots, 3000}$ sadrži $3$ elementa od kojih su svaka $2$ međusobno relativno prosta.
Izvor: Kamp 2013. - Kombinatorika, M. M.