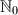
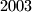
U vrhovima pravilnog šesterokuta upisano je šest brojeva iz čija je suma . Branko ponavlja ovakve poteze: odabire jedan vrh i zamjenjuje broj u tom vrhu apsolutnom vrijednošću razlike brojeva u dva susjedna vrha. Dokažite da Branko može postići da nakon konačnog broja poteza u svim vrhovima bude .
%V0
U vrhovima pravilnog šesterokuta upisano je šest brojeva iz $\mathbb{N}_0$ čija je suma $2003$. Branko ponavlja ovakve poteze: odabire jedan vrh i zamjenjuje broj u tom vrhu apsolutnom vrijednošću razlike brojeva u dva susjedna vrha. Dokažite da Branko može postići da nakon konačnog broja poteza u svim vrhovima bude $0$.
Školjka 
čija je suma 
. Branko ponavlja ovakve poteze: odabire jedan vrh i zamjenjuje broj u tom vrhu apsolutnom vrijednošću razlike brojeva u dva susjedna vrha. Dokažite da Branko može postići da nakon konačnog broja poteza u svim vrhovima bude 
.