U šesterokutu
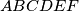
vrijedi

Ako su duljine stranica tog šesterokuta prirodni brojevi, dokaži da ne mogu svi biti neparni.
%V0
U šesterokutu $ABCDEF$ vrijedi $$ AB \perp BC \text{,} \qquad AC \perp CD \text{,} \qquad AD \perp DE \text{,} \qquad AE \perp EF \text{.} $$ Ako su duljine stranica tog šesterokuta prirodni brojevi, dokaži da ne mogu svi biti neparni.