Kamp '13 - Funkcije, napredna - Uvod
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Neki pojmovi vezani uz funkcije:
Za funkciju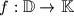 kažemo da je injekcija ako vrijedi:
kažemo da je injekcija ako vrijedi: 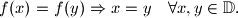
Za funkciju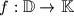 kažemo da je surjekcija ako vrijedi:
kažemo da je surjekcija ako vrijedi: 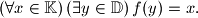
Za funkciju kažemo da bijekcija ako je i injekcija i surjekcija.
Funkcija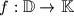 je parna ako je
je parna ako je 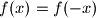 za svaki
za svaki 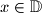 , a neparna ako je
, a neparna ako je 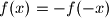 za svaki
za svaki 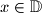 . To svojstvo zovemo parnost. Funkcija ne mora nužno imati parnost.
. To svojstvo zovemo parnost. Funkcija ne mora nužno imati parnost.
Funkcija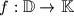 je periodična ako postoji
je periodična ako postoji 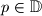 takav da
takav da 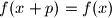 za svaki
za svaki 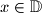 . Takav
. Takav  zovemo periodom funkcije
zovemo periodom funkcije  .
.
Za funkciju
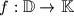 kažemo da je injekcija ako vrijedi:
kažemo da je injekcija ako vrijedi: 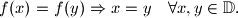
Za funkciju
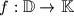 kažemo da je surjekcija ako vrijedi:
kažemo da je surjekcija ako vrijedi: 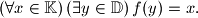
Za funkciju kažemo da bijekcija ako je i injekcija i surjekcija.
Funkcija
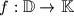 je parna ako je
je parna ako je 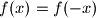 za svaki
za svaki 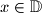 , a neparna ako je
, a neparna ako je 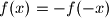 za svaki
za svaki 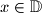 . To svojstvo zovemo parnost. Funkcija ne mora nužno imati parnost.
. To svojstvo zovemo parnost. Funkcija ne mora nužno imati parnost.Funkcija
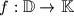 je periodična ako postoji
je periodična ako postoji 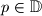 takav da
takav da 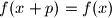 za svaki
za svaki 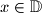 . Takav
. Takav  zovemo periodom funkcije
zovemo periodom funkcije  .
. Izvor: Kamp 2013. - Funkcije, napredna grupa, V. S.
 Školjka
Školjka 
