Kamp '13 - Funkcije, napredna 7.
Dodao/la:
arhiva3. studenoga 2013. Nađite sve funkcije
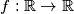
takve da je
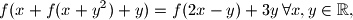
uz uvjet da je

injektivan.
%V0
Nađite sve funkcije $f : \mathbb{R} \rightarrow \mathbb{R}$ takve da je $$f(x+f(x+y^2)+y)=f(2x-y) + 3y \, \forall x, y \in \mathbb{R}\text{,}$$ uz uvjet da je $f$ injektivan.
Izvor: Kamp 2013. - Funkcije, napredna grupa, V. S.