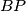
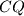
Neka je trokut, a centar njemu opisane kružnice. i su redom na i . Kružnica prolazi redom kroz polovišta , i . Pokaži da ako je tangenta na tada je .
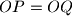
%V0
Neka je $ABC$ trokut, a $O$ centar njemu opisane kružnice. $P$ i $Q$ su redom na $CA$ i $AB$. Kružnica $k$ prolazi redom kroz polovišta $BP$, $CQ$ i $PQ$. Pokaži da ako je $PQ$ tangenta na $k$ tada je $OP = OQ$.
Školjka 
trokut, a 
centar njemu opisane kružnice. 
i 
su redom na 
i 
. Kružnica 
prolazi redom kroz polovišta 
, 
i 
. Pokaži da ako je 
.