Kamp '13 - Geometrija 14.
Dodao/la:
arhiva3. studenoga 2013. Neka je točka

unutar

. Pravci
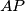
,
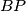
,
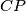
sijeku opisanu kružnicu

u redom

,

,

. Tangenta na opisanu kružnicu u

siječe

u

. Dokaži da
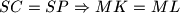
.
%V0
Neka je točka $P$ unutar $ABC$. Pravci $AP$, $BP$, $CP$ sijeku opisanu kružnicu $ABC$ u redom $K$, $L$, $M$. Tangenta na opisanu kružnicu u $C$ siječe $AB$ u $S$. Dokaži da $SC = SP \Rightarrow MK = ML$.
Izvor: Kamp 2013. - Geometrija, M. M.