Sve točke ravnine su na bilo koji način podijeljene na dva disjunktna skupa. Dokažite da postoji trokut čiji vrhovi pripadaju istom skupu, najmanja stranica mu ima duljinu

i kutovi mu se odnose kao
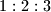
.
%V0
Sve točke ravnine su na bilo koji način podijeljene na dva disjunktna skupa. Dokažite da postoji trokut čiji vrhovi pripadaju istom skupu, najmanja stranica mu ima duljinu $1$ i kutovi mu se odnose kao $1:2:3$.