Neka je

kompleksan broj i
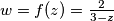
.
(a) Odredite skup
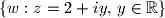
u kompleksnoj ravnini.
(b) Pokažite da se funkcija

može zapisati u obliku
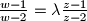
.
(c) Neka je
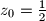
i niz
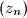
definiran sa
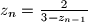
,
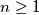
.
Koristeći svojstvo (b) izračunajte limes niza
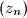
.
%V0
Neka je $z$ kompleksan broj i $w = f(z) = \frac{2}{3-z}$.
(a) Odredite skup $\{w : z=2+iy,\, y \in \mathbb{R}\}$ u kompleksnoj ravnini.
(b) Pokažite da se funkcija $w$ može zapisati u obliku $\frac{w-1}{w-2}=\lambda \frac{z-1}{z-2}$.
(c) Neka je $z_0 = \frac12$ i niz $(z_n)$ definiran sa
$z_n = \frac{2}{3-z_{n-1}}$, $n \geq 1$.
Koristeći svojstvo (b) izračunajte limes niza $(z_n)$.