1 - Prebrojavanje Uvod
Kvaliteta:
Avg: 4,5Težina:
Avg: 0,0 U ovom predavanju bavit ćemo se brojanjem koliko ima objekata nekog tipa, ili na koliko načina neke objekte možemo poredati u niz.
Prvo je najjednostavnije pitanje - ako imamo različitih štapića, na koliko ih različitih načina možemo poredati u niz.
različitih štapića, na koliko ih različitih načina možemo poredati u niz.
Ako odaberemo koji će nam štapić biti prvi (što možemo napraviti na različitih načina) dolazimo do istog problema s
različitih načina) dolazimo do istog problema s  štapićem, vidimo da će ukupno rješenje biti
štapićem, vidimo da će ukupno rješenje biti 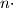 broj načina da poredamo
broj načina da poredamo  štapić.
štapić.
Ponovnom primjenom iste logike, možemo odabrati koji će nam biti drugi štapić po redu na načina, pa je sada pitanje na koliko načina možemo poredati njih
načina, pa je sada pitanje na koliko načina možemo poredati njih  , a ukupni rezultat će biti
, a ukupni rezultat će biti 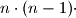 broj načina da se poreda
broj načina da se poreda  štapića.
štapića.
Jasno je da daljnjim ponavljanjem istoga dolazimo do toga da je traženi broj načina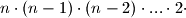 broj načina da poredamo
broj načina da poredamo  štapić.
štapić.
Ali broj načina da poredamo štapić u niz je očito
štapić u niz je očito  .
.
Dakle, broj načina da poredamo štapića u niz je
štapića u niz je 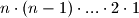 .
.
Taj broj označavamo oznakom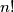 , a izgovaramo
, a izgovaramo  faktorijela.
faktorijela.
Drugo je pitanje, ako imamo međusobno različitih kuglica, na koliko načina možemo odabrati njih
međusobno različitih kuglica, na koliko načina možemo odabrati njih  (u ovom nam slučaju redoslijed odabira nije važan).
(u ovom nam slučaju redoslijed odabira nije važan).
Prvu kuglicu možemo odabrati na načina, drugu na
načina, drugu na  načina, i tako dalje,
načina, i tako dalje,  -tu možemo odabrati na
-tu možemo odabrati na 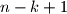 načina. Dakle, ukupan broj načina je
načina. Dakle, ukupan broj načina je 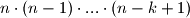 .
.
No rekli smo da je redoslijed odabira nevažan, pa zato sada još trebamo odrediti koliko smo puta svaki od tih skupova kuglica odabrali. To možemo odrediti tako da izračunamo na koliko načina tih kuglica možemo posložiti u niz.
kuglica možemo posložiti u niz.
Gore otkrili da taj broj iznosi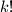 .
.
Dakle, ukupan broj načina za odabrati kuglica od njih
kuglica od njih  je
je 
No, kako je to neuredno zapisivati, proširimo cijeli razlomak s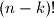 i tako dobivamo
i tako dobivamo
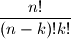
Ovaj broj označavamo s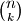 , a izgovaramo
, a izgovaramo  povrh k. Oznaka
povrh k. Oznaka 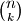 je poznata i pod nazivom binomni koeficijent.
je poznata i pod nazivom binomni koeficijent.
Prvo je najjednostavnije pitanje - ako imamo
 različitih štapića, na koliko ih različitih načina možemo poredati u niz.
različitih štapića, na koliko ih različitih načina možemo poredati u niz.Ako odaberemo koji će nam štapić biti prvi (što možemo napraviti na
 različitih načina) dolazimo do istog problema s
različitih načina) dolazimo do istog problema s  štapićem, vidimo da će ukupno rješenje biti
štapićem, vidimo da će ukupno rješenje biti 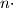 broj načina da poredamo
broj načina da poredamo  štapić.
štapić.Ponovnom primjenom iste logike, možemo odabrati koji će nam biti drugi štapić po redu na
 načina, pa je sada pitanje na koliko načina možemo poredati njih
načina, pa je sada pitanje na koliko načina možemo poredati njih  , a ukupni rezultat će biti
, a ukupni rezultat će biti 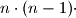 broj načina da se poreda
broj načina da se poreda  štapića.
štapića.Jasno je da daljnjim ponavljanjem istoga dolazimo do toga da je traženi broj načina
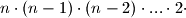 broj načina da poredamo
broj načina da poredamo  štapić.
štapić.Ali broj načina da poredamo
 štapić u niz je očito
štapić u niz je očito  .
. Dakle, broj načina da poredamo
 štapića u niz je
štapića u niz je 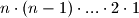 .
.Taj broj označavamo oznakom
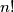 , a izgovaramo
, a izgovaramo  faktorijela.
faktorijela.Drugo je pitanje, ako imamo
 međusobno različitih kuglica, na koliko načina možemo odabrati njih
međusobno različitih kuglica, na koliko načina možemo odabrati njih  (u ovom nam slučaju redoslijed odabira nije važan).
(u ovom nam slučaju redoslijed odabira nije važan).Prvu kuglicu možemo odabrati na
 načina, drugu na
načina, drugu na  načina, i tako dalje,
načina, i tako dalje,  -tu možemo odabrati na
-tu možemo odabrati na 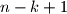 načina. Dakle, ukupan broj načina je
načina. Dakle, ukupan broj načina je 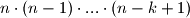 .
.No rekli smo da je redoslijed odabira nevažan, pa zato sada još trebamo odrediti koliko smo puta svaki od tih skupova kuglica odabrali. To možemo odrediti tako da izračunamo na koliko načina tih
 kuglica možemo posložiti u niz.
kuglica možemo posložiti u niz. Gore otkrili da taj broj iznosi
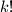 .
.Dakle, ukupan broj načina za odabrati
 kuglica od njih
kuglica od njih  je
je 
No, kako je to neuredno zapisivati, proširimo cijeli razlomak s
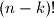 i tako dobivamo
i tako dobivamo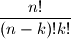
Ovaj broj označavamo s
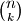 , a izgovaramo
, a izgovaramo  povrh k. Oznaka
povrh k. Oznaka 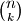 je poznata i pod nazivom binomni koeficijent.
je poznata i pod nazivom binomni koeficijent.  Školjka
Školjka 
