1 - Sustavi Ostataka
Kvaliteta:
Avg: 5,0Težina:
Avg: 0,0 U ovom poglavlju očekuje se znanje predavanja kongruencije.
Skup ćemo nazivati potpuni sustav ostataka modulo n ako elementi
ćemo nazivati potpuni sustav ostataka modulo n ako elementi  svi daju različite ostatke pri dijeljenju s
svi daju različite ostatke pri dijeljenju s  , i svi ostatci će pojavljuju.
, i svi ostatci će pojavljuju.
Za razmisliti: koliko elemenata ima svaki potpuni sustav ostataka modulo , za neki fiksni
, za neki fiksni  ?
?
Skup ćemo nazivati reducirani sustav ostataka modulo n ako svi elementi
ćemo nazivati reducirani sustav ostataka modulo n ako svi elementi  daju različite ostatke pri dijeljenju s
daju različite ostatke pri dijeljenju s  i pojavljuju se svi ostaci koji su relativno prosti s
i pojavljuju se svi ostaci koji su relativno prosti s  .
.
Primjer:
Potpuni sustav ostataka modulo je
je 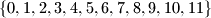
Reducirani sustav ostataka modulo je
je 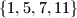
Primjetimo da je za prost broj potpuni sustav ostataka
potpuni sustav ostataka 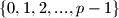 , a reducirani sustav ostataka
, a reducirani sustav ostataka 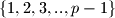 . Ovo vrijedi jer je
. Ovo vrijedi jer je  relativno prost sa svim brojevima manjima od sebe.
relativno prost sa svim brojevima manjima od sebe.
Inverz
Sada se vratimo na pitanje koje smo ostavili otvoreno u poglavlju kongruencije. Pitanje dijeljenja.
Zapazimo da dijeljenje s nije ništa drugo nego množenje s
nije ništa drugo nego množenje s  , to jest ako želimo podijeliti neki broj s
, to jest ako želimo podijeliti neki broj s  , zapravo ga želimo pomnožiti s nekim
, zapravo ga želimo pomnožiti s nekim  takvim da
takvim da 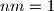 .
.
Ovako odabrani zovemo inverz broja
zovemo inverz broja  (primijetimo i da je
(primijetimo i da je  inverz od
inverz od  ).
).
Sada se postavlja prirodno pitanje, ako promatramo neki fiksni modul , ima li svaki broj
, ima li svaki broj  svoj inverz modulo
svoj inverz modulo  ?
?
Tu odmah vidimo da je odgovor ne, jer primjerice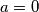 očito nema inverz.
očito nema inverz.
No može se pokazati da ako vrijedi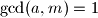 da
da  ima jedinstveni inverz modulo
ima jedinstveni inverz modulo  . To će biti direktna posljedica zadatka
. To će biti direktna posljedica zadatka  iz ovog područja.
iz ovog područja.
Što to zapravo znači?
Ono što to za nas znači u praktičnom smislu je da, ako imamo kongruencijsku jednadžbu, i neki relativno prost s
relativno prost s  , tada možemo čitavu jednadžbu podijeliti s
, tada možemo čitavu jednadžbu podijeliti s  .
.
Skup
 ćemo nazivati potpuni sustav ostataka modulo n ako elementi
ćemo nazivati potpuni sustav ostataka modulo n ako elementi  svi daju različite ostatke pri dijeljenju s
svi daju različite ostatke pri dijeljenju s  , i svi ostatci će pojavljuju.
, i svi ostatci će pojavljuju. Za razmisliti: koliko elemenata ima svaki potpuni sustav ostataka modulo
 , za neki fiksni
, za neki fiksni  ?
?Skup
 ćemo nazivati reducirani sustav ostataka modulo n ako svi elementi
ćemo nazivati reducirani sustav ostataka modulo n ako svi elementi  daju različite ostatke pri dijeljenju s
daju različite ostatke pri dijeljenju s  i pojavljuju se svi ostaci koji su relativno prosti s
i pojavljuju se svi ostaci koji su relativno prosti s  .
.Primjer:
Potpuni sustav ostataka modulo
 je
je 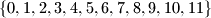
Reducirani sustav ostataka modulo
 je
je 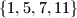
Primjetimo da je za prost broj
 potpuni sustav ostataka
potpuni sustav ostataka 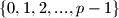 , a reducirani sustav ostataka
, a reducirani sustav ostataka 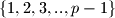 . Ovo vrijedi jer je
. Ovo vrijedi jer je  relativno prost sa svim brojevima manjima od sebe.
relativno prost sa svim brojevima manjima od sebe.Inverz
Sada se vratimo na pitanje koje smo ostavili otvoreno u poglavlju kongruencije. Pitanje dijeljenja.
Zapazimo da dijeljenje s
 nije ništa drugo nego množenje s
nije ništa drugo nego množenje s  , to jest ako želimo podijeliti neki broj s
, to jest ako želimo podijeliti neki broj s  , zapravo ga želimo pomnožiti s nekim
, zapravo ga želimo pomnožiti s nekim  takvim da
takvim da 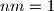 .
.Ovako odabrani
 zovemo inverz broja
zovemo inverz broja  (primijetimo i da je
(primijetimo i da je  inverz od
inverz od  ).
).Sada se postavlja prirodno pitanje, ako promatramo neki fiksni modul
 , ima li svaki broj
, ima li svaki broj  svoj inverz modulo
svoj inverz modulo  ?
?Tu odmah vidimo da je odgovor ne, jer primjerice
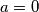 očito nema inverz.
očito nema inverz.No može se pokazati da ako vrijedi
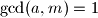 da
da  ima jedinstveni inverz modulo
ima jedinstveni inverz modulo  . To će biti direktna posljedica zadatka
. To će biti direktna posljedica zadatka  iz ovog područja.
iz ovog područja. Što to zapravo znači?
Ono što to za nas znači u praktičnom smislu je da, ako imamo kongruencijsku jednadžbu, i neki
 relativno prost s
relativno prost s  , tada možemo čitavu jednadžbu podijeliti s
, tada možemo čitavu jednadžbu podijeliti s  .
.  Školjka
Školjka 
