u ravnini je dan kvadrat s vrhovima
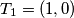
,
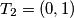
,
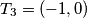
,
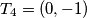
. za svaki

neka je
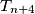
poloviste duzine
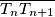
. uz pretpostavku da niz tocaka
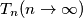
ima granicnu tocku, nadite koordinate te tocke.
%V0
u ravnini je dan kvadrat s vrhovima $T_1 = (1, 0)$, $T_2 = (0, 1)$, $T_3 = (-1, 0)$, $T_4 = (0, -1)$. za svaki $n \in \mathbb{N}$ neka je $T_{n+4}$ poloviste duzine $\overline{T_nT_{n+1}}$. uz pretpostavku da niz tocaka $T_n (n \rightarrow \infty)$ ima granicnu tocku, nadite koordinate te tocke.