Slični zadaci
Osim žarulja poredano je u krug. Svaka žarulja može biti ili upaljena ili ugašena. U jednom koraku radimo sljedeću transformaciju: žarulja će nakon transformacija biti ugašena, ukoliko je jedna od njoj susjednih žarulja upaljena, a druga ugašena, odnosno, žarulja će nakon transformacije svijetliti, ukoliko su obje njoj susjedne žarulje ili upaljene ili ugašene. U jednom se koraku na stanja svih žarulja djeluje istovremeno.
Dokažite da će, nakon najviše četiri koraka, sve žarulje svijetliti.
Dokažite da će, nakon najviše četiri koraka, sve žarulje svijetliti.
 Školjka
Školjka  ispunjena je jedinicama i nulama. Poznate je da ne postoje četiri jedinice na mjestima koje čine pravokutnik. Dokažite da je broj jedinica u tablici najviše
ispunjena je jedinicama i nulama. Poznate je da ne postoje četiri jedinice na mjestima koje čine pravokutnik. Dokažite da je broj jedinica u tablici najviše 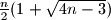 .
. 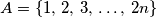 i funkcija
i funkcija 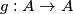 definirana sa
definirana sa 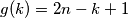 . Da li postoji funkcija
. Da li postoji funkcija 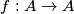 takva da je
takva da je 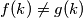 za svaki
za svaki 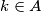 i
i 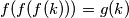 za svaki
za svaki 
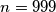 ,
,
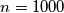 ?
?  pozitivan cijeli broj veci od
pozitivan cijeli broj veci od  . koliko ima permutacija
. koliko ima permutacija 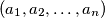 brojeva
brojeva  ,
,  ,
, 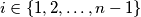 za koji je
za koji je 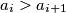
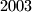 poredani su u niz. na nizu vrsimo ovu operaciju: ako je prvi broj u nizu jednak
poredani su u niz. na nizu vrsimo ovu operaciju: ako je prvi broj u nizu jednak  , okrenemo poredak prvih
, okrenemo poredak prvih 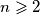 , potrebno je upisati brojeve
, potrebno je upisati brojeve  i
i  tako da svaka četiri polja koja imaju jedan zajednički vrh sadrže četiri različita broja.
tako da svaka četiri polja koja imaju jedan zajednički vrh sadrže četiri različita broja.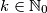 moguće odabrati
moguće odabrati 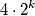 različitih prirodnih brojeva koji nisu veći od
različitih prirodnih brojeva koji nisu veći od 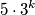 , tako da među njima ne postoje tri uzastopna člana aritmetičkog niza.
, tako da među njima ne postoje tri uzastopna člana aritmetičkog niza.