neka je
prirodan broj i neka su
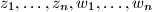
kompleksni brojevi takvi da za svaki izbor brojeva
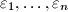
iz skupa
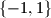
vrijedi
.
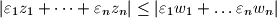
dokazite da je
.
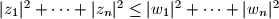
%V0
neka je $n$ prirodan broj i neka su $z_1, \dots, z_n, w_1, \dots, w_n$ kompleksni brojevi takvi da za svaki izbor brojeva $\varepsilon_1, \dots, \varepsilon_n$ iz skupa $\{-1, 1\}$ vrijedi
$|\varepsilon_1z_1 + \dots + \varepsilon_nz_n| \leq |\varepsilon_1w_1 + \dots \varepsilon_nw_n|$.
dokazite da je
$|z_1|^2 + \dots + |z_n|^2 \leq |w_1|^2 + \dots + |w_n|^2$.
Školjka