niz
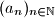
je zadan rekurzivno s
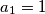
,
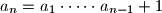
, za

.
odredite najmanji realni broj

takav da je
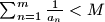
za svaki
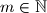
.
%V0
niz $(a_n)_{n\in\mathbb{N}}$ je zadan rekurzivno s $a_1 = 1$,
$a_n = a_1 \cdot \dots \cdot a_{n-1} + 1$, za $n \geq 2$.
odredite najmanji realni broj $M$ takav da je
$\sum_{n=1}^m \frac{1}{a_n} < M$ za svaki $m \in \mathbb{N}$.