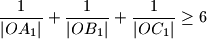Slični zadaci
Kružnice  i
i  sijeku se u točkama
sijeku se u točkama  i
i  . Tangenta kružnice
. Tangenta kružnice  povučena iz točke
povučena iz točke
 siječe kružnicu
siječe kružnicu  u točki
u točki  , a tangenta kružnice
, a tangenta kružnice  povućena iz točke
povućena iz točke  siječe
siječe
kružnicu u točki
u točki  . Polupravac kroz točku
. Polupravac kroz točku  , koji leži unutar kuta
, koji leži unutar kuta 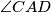 ,
,
siječe kružnicu u točki
u točki  , kružnicu
, kružnicu  u točki
u točki  i kružnicu opisanu trokutu
i kružnicu opisanu trokutu
 u točki
u točki  . Dokaži da je udaljenost točaka
. Dokaži da je udaljenost točaka  i
i  jednaka udaljenosti točaka
jednaka udaljenosti točaka
 i
i  .
.
 i
i  sijeku se u točkama
sijeku se u točkama  i
i  . Tangenta kružnice
. Tangenta kružnice  povučena iz točke
povučena iz točke siječe kružnicu
siječe kružnicu  u točki
u točki  , a tangenta kružnice
, a tangenta kružnice  povućena iz točke
povućena iz točke  siječe
siječekružnicu
 u točki
u točki  . Polupravac kroz točku
. Polupravac kroz točku  , koji leži unutar kuta
, koji leži unutar kuta 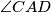 ,
,siječe kružnicu
 u točki
u točki  , kružnicu
, kružnicu  u točki
u točki  i kružnicu opisanu trokutu
i kružnicu opisanu trokutu u točki
u točki  . Dokaži da je udaljenost točaka
. Dokaži da je udaljenost točaka  i
i  jednaka udaljenosti točaka
jednaka udaljenosti točaka i
i  .
. Šest otoka povezano je linijama jednog trajektnog i jednog hidrogliserskog poduzeća. Svaka dva otoka povezana su (u oba smjera) linijom točno jednog od ova dva poduzeća. Dokaži da je moguće ciklički posjetiti četiri otoka koristeći linije samo jednog poduzeća (tj. da postoje četiri otoka 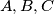 i
i  i poduzeće čiji brodovi plove na linijama
i poduzeće čiji brodovi plove na linijama 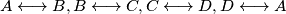 ).
).
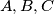 i
i  i poduzeće čiji brodovi plove na linijama
i poduzeće čiji brodovi plove na linijama 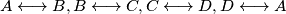 ).
).  Školjka
Školjka  i
i  prirodni brojevi, dokaži da je izraz
prirodni brojevi, dokaži da je izraz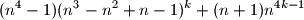 djeljiv s
djeljiv s 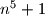 .
. 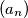 zadan je rekurzivno:
zadan je rekurzivno: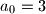

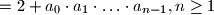 .
.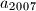 .
. 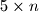 kojoj je svako polje obojano u crvenu ili plavu boju. Nađite najmanji
kojoj je svako polje obojano u crvenu ili plavu boju. Nađite najmanji  polja u njihovom presjeku iste boje.
polja u njihovom presjeku iste boje.  kome su
kome su  ,
,  i
i  ,
,  i
i  upisan je u kružnicu sa središtem u točki
upisan je u kružnicu sa središtem u točki  polumjera
polumjera  . Dokažite da je
. Dokažite da je