Neka su
,
i
pozitivni realni brojevi takvi da je
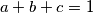
. Dokaži da vrijedi
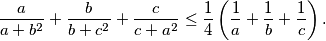
%V0
Neka su $a$, $b$ i $c$ pozitivni realni brojevi takvi da je $a + b + c = 1$. Dokaži da vrijedi $$
\frac{a}{a + b^2} +
\frac{b}{b + c^2} +
\frac{c}{c + a^2} \leq
\frac14 \left( \frac1a + \frac1b + \frac1c \right) \text{.}
$$
Školjka