Simulacija županijskog 2016. za prvi razred zadatak 5.
Kvaliteta:
Avg: 4,0Težina:
Avg: 4,0Izvor: Simulacija županijskog 2016. za prvi razred
Komentari:
Daniel_Sirola, 17. veljače 2016. 20:33
ikicic, 16. veljače 2016. 15:47
MNM, 16. veljače 2016. 15:30
Vjerojatno si ga dobro shvatio, i onda odgovor je da se gleda samo relativna prostost u parovima. Doduše, nebi bilo dobro da je u tekstu zadatka pisalo "sa zajedničkom stranicom". Dakle, svaki broj koji nije na rubu tablice je relativno prost s  drugih brojeva, svaki koji je na rubu a nije na kutu sa njih
drugih brojeva, svaki koji je na rubu a nije na kutu sa njih  , a ova četiri u kutu sa njih
, a ova četiri u kutu sa njih  .
.
 drugih brojeva, svaki koji je na rubu a nije na kutu sa njih
drugih brojeva, svaki koji je na rubu a nije na kutu sa njih  , a ova četiri u kutu sa njih
, a ova četiri u kutu sa njih  .
. ikicic, 16. veljače 2016. 12:43
lkkraljevic, 16. veljače 2016. 10:41
MNM, 16. veljače 2016. 10:10
Ako brojevi dijele vrh tada su relativno prosti. Dakle, uvjet je da brojevi budu samo u parovima relativno prosti. Teško je reći što tebi znače 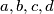 koje si napisao, ali možda bi se to u tvojoj terminologiji moglo shvatiti kao ovo drugo, tj.
koje si napisao, ali možda bi se to u tvojoj terminologiji moglo shvatiti kao ovo drugo, tj. 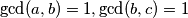 itd. (dakle
itd. (dakle  i
i  , te
, te  i
i  su sad ti brojevi koji dijele vrh). Također, malo je upitno zašto si napisao samo
su sad ti brojevi koji dijele vrh). Također, malo je upitno zašto si napisao samo  broja, naime "većina", tj. sva unutrašnja polja imaju po
broja, naime "većina", tj. sva unutrašnja polja imaju po  susjednih polja s kojima dijele vrh (primjeti da ako dijele stranicu, dijele čak
susjednih polja s kojima dijele vrh (primjeti da ako dijele stranicu, dijele čak  vrha).
vrha).
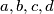 koje si napisao, ali možda bi se to u tvojoj terminologiji moglo shvatiti kao ovo drugo, tj.
koje si napisao, ali možda bi se to u tvojoj terminologiji moglo shvatiti kao ovo drugo, tj. 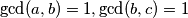 itd. (dakle
itd. (dakle  i
i  , te
, te  i
i  su sad ti brojevi koji dijele vrh). Također, malo je upitno zašto si napisao samo
su sad ti brojevi koji dijele vrh). Također, malo je upitno zašto si napisao samo  broja, naime "većina", tj. sva unutrašnja polja imaju po
broja, naime "većina", tj. sva unutrašnja polja imaju po  susjednih polja s kojima dijele vrh (primjeti da ako dijele stranicu, dijele čak
susjednih polja s kojima dijele vrh (primjeti da ako dijele stranicu, dijele čak  vrha).
vrha). Daniel_Sirola, 15. veljače 2016. 23:04
Zadnja promjena: Daniel_Sirola, 15. veljače 2016. 23:04
 Školjka
Školjka 

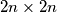 upisani su prirodni brojevi od 1 do 10, pri čemu su brojevi u poljima sa zajedničkim vrhom relativno prosti. Dokažite da postoji broj koji se u tablici pojavljuje barem
upisani su prirodni brojevi od 1 do 10, pri čemu su brojevi u poljima sa zajedničkim vrhom relativno prosti. Dokažite da postoji broj koji se u tablici pojavljuje barem 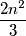 puta.
puta. 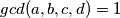 ili je svaki broj sa svakim relativno prost,
ili je svaki broj sa svakim relativno prost, 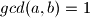 i
i 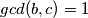 itd. ...?
itd. ...?