Dani su realni brojevi
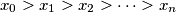
. Dokaži da je
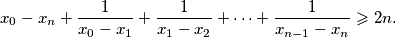
Kada vrijedi jednakost?
%V0
Dani su realni brojevi $x_{0} > x_{1} > x_{2} > \cdots > x_{n}$. Dokaži da je $$ x_{0} - x_{n} + \frac{1}{x_{0} - x_{1}} + \frac{1}{x_{1} - x_{2}} + \cdots + \frac{1}{x_{n - 1} - x_{n}} \geqslant 2n \text{.} $$
Kada vrijedi jednakost?