Slični zadaci
Dva igrača,  i
i  igraju sljedeću igru:
igraju sljedeću igru:  i
i  zapisuju naizmjenično po jednu znamenku sve dok ne napišu šesteroznamenkasti broj, pri čemu se niti jedna znamenka ne smije ponoviti. Prva znamenka mora biti različita od
zapisuju naizmjenično po jednu znamenku sve dok ne napišu šesteroznamenkasti broj, pri čemu se niti jedna znamenka ne smije ponoviti. Prva znamenka mora biti različita od  . Igrač
. Igrač  igra prvi, a znamenke se pišu redom slijeva nadesno. Igrač
igra prvi, a znamenke se pišu redom slijeva nadesno. Igrač  pobjeđuje ako je napisani šesteroznamenkasti broj djeljiv s
pobjeđuje ako je napisani šesteroznamenkasti broj djeljiv s  ,
,  ili
ili  , a u suprotnom pobjeđuje igrač
, a u suprotnom pobjeđuje igrač  . Dokaži da igrač
. Dokaži da igrač  ima strategiju za pobjedu, tj. može pobijediti neovisno o igri igrača
ima strategiju za pobjedu, tj. može pobijediti neovisno o igri igrača  .
.
 i
i  igraju sljedeću igru:
igraju sljedeću igru:  i
i  zapisuju naizmjenično po jednu znamenku sve dok ne napišu šesteroznamenkasti broj, pri čemu se niti jedna znamenka ne smije ponoviti. Prva znamenka mora biti različita od
zapisuju naizmjenično po jednu znamenku sve dok ne napišu šesteroznamenkasti broj, pri čemu se niti jedna znamenka ne smije ponoviti. Prva znamenka mora biti različita od  . Igrač
. Igrač  igra prvi, a znamenke se pišu redom slijeva nadesno. Igrač
igra prvi, a znamenke se pišu redom slijeva nadesno. Igrač  pobjeđuje ako je napisani šesteroznamenkasti broj djeljiv s
pobjeđuje ako je napisani šesteroznamenkasti broj djeljiv s  ,
,  ili
ili  , a u suprotnom pobjeđuje igrač
, a u suprotnom pobjeđuje igrač  . Dokaži da igrač
. Dokaži da igrač  ima strategiju za pobjedu, tj. može pobijediti neovisno o igri igrača
ima strategiju za pobjedu, tj. može pobijediti neovisno o igri igrača  .
.  Školjka
Školjka  pravokutna ploča
pravokutna ploča 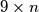 može prekriti pločicama oblika
može prekriti pločicama oblika  tako da se one međusobno ne preklapaju?
tako da se one međusobno ne preklapaju?  rečenica lijevo od ove kartice je lažno., za
rečenica lijevo od ove kartice je lažno., za 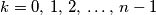 . Kartice su složene u nekom redoslijedu slijeva nadesno. Koliko najviše rečenica može biti istinito?
. Kartice su složene u nekom redoslijedu slijeva nadesno. Koliko najviše rečenica može biti istinito?  ,
,  ,
,  ,
,  ,
,  ,
,  , ... konstruira se tako da je svaki broj, počevši od petog, jednak znamenki jedinica zbroja prethodne četiri znamenke.
, ... konstruira se tako da je svaki broj, počevši od petog, jednak znamenki jedinica zbroja prethodne četiri znamenke.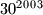 koji nisu djelitelji broja
koji nisu djelitelji broja 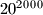 ?
?  ,
,  ,
,  lipa i od
lipa i od  lipa može isplatiti pomoću
lipa može isplatiti pomoću  kovanica, onda se iznos od
kovanica, onda se iznos od 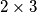 pravokutniku točno dva kvadratića su crvena. Promatrajte bilo koji
pravokutniku točno dva kvadratića su crvena. Promatrajte bilo koji 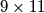 pravokutnik. Koliko u njemu ima crvenih kvadratića?
pravokutnik. Koliko u njemu ima crvenih kvadratića?