Za rastavljanje šahovske ploče dimenzija 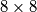 na disjunktne pravokutnike kažemo da je raznovrsno ako su ispunjena sljedeća dva uvjeta:
na disjunktne pravokutnike kažemo da je raznovrsno ako su ispunjena sljedeća dva uvjeta:
 svaki pravokutnik u rastavu sadrži jednak broj crnih i bijelih polja;
svaki pravokutnik u rastavu sadrži jednak broj crnih i bijelih polja;
 ne postoje dva pravokutnika koja sadrže isti broj polja.
ne postoje dva pravokutnika koja sadrže isti broj polja.
Odredi najveći prirodni broj  za koji postoji raznovrsno rastavljanje ploče dimenzija
za koji postoji raznovrsno rastavljanje ploče dimenzija 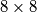 na
na  pravokutnika.
pravokutnika.
Za rastavljanje šahovske ploče dimenzija $8 \times 8$ na disjunktne pravokutnike kažemo da je
raznovrsno ako su ispunjena sljedeća dva uvjeta:
$\text{(i)}$ svaki pravokutnik u rastavu sadrži jednak broj crnih i bijelih polja;
$\text{(ii)}$ ne postoje dva pravokutnika koja sadrže isti broj polja.
Odredi najveći prirodni broj $n$ za koji postoji raznovrsno rastavljanje ploče dimenzija
$8 \times 8$ na $n$ pravokutnika.
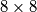 na disjunktne pravokutnike kažemo da je raznovrsno ako su ispunjena sljedeća dva uvjeta:
na disjunktne pravokutnike kažemo da je raznovrsno ako su ispunjena sljedeća dva uvjeta: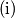 svaki pravokutnik u rastavu sadrži jednak broj crnih i bijelih polja;
svaki pravokutnik u rastavu sadrži jednak broj crnih i bijelih polja;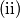 ne postoje dva pravokutnika koja sadrže isti broj polja.
ne postoje dva pravokutnika koja sadrže isti broj polja. za koji postoji raznovrsno rastavljanje ploče dimenzija
za koji postoji raznovrsno rastavljanje ploče dimenzija 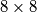 na
na  pravokutnika.
pravokutnika.  Školjka
Školjka