Slični zadaci
Na ploču 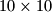 postavljeno je
postavljeno je  žetona tako da nikoja dva nisu na istom polju. Pritom
žetona tako da nikoja dva nisu na istom polju. Pritom 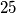 žetona zauzima donju lijevu četvrtinu ploče, a preostalih
žetona zauzima donju lijevu četvrtinu ploče, a preostalih 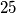 gornju desnu četvrtinu. Neka su
gornju desnu četvrtinu. Neka su  ,
,  ,
,  redom tri uzastopna polja (horizontalno, vertikalno ili dijagonalno). Ako se dva žetona nalaze na poljima
redom tri uzastopna polja (horizontalno, vertikalno ili dijagonalno). Ako se dva žetona nalaze na poljima  i
i  i ako je polje
i ako je polje  slobodno, žeton s polja
slobodno, žeton s polja  može se premjestiti na polje
može se premjestiti na polje  , preskočivši žeton na polju
, preskočivši žeton na polju  .
.
Može li se, konačnim nizom takvih poteza, premjestiti svih žetona na donju polovicu ploče?
žetona na donju polovicu ploče?
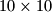 postavljeno je
postavljeno je  žetona tako da nikoja dva nisu na istom polju. Pritom
žetona tako da nikoja dva nisu na istom polju. Pritom 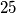 žetona zauzima donju lijevu četvrtinu ploče, a preostalih
žetona zauzima donju lijevu četvrtinu ploče, a preostalih 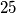 gornju desnu četvrtinu. Neka su
gornju desnu četvrtinu. Neka su  ,
,  ,
,  redom tri uzastopna polja (horizontalno, vertikalno ili dijagonalno). Ako se dva žetona nalaze na poljima
redom tri uzastopna polja (horizontalno, vertikalno ili dijagonalno). Ako se dva žetona nalaze na poljima  i
i  i ako je polje
i ako je polje  slobodno, žeton s polja
slobodno, žeton s polja  može se premjestiti na polje
može se premjestiti na polje  , preskočivši žeton na polju
, preskočivši žeton na polju  .
.Može li se, konačnim nizom takvih poteza, premjestiti svih
 žetona na donju polovicu ploče?
žetona na donju polovicu ploče? Prijateljice Anica i Neda igraju igru tako da u svakom potezu, nakon što jedna od njih kaže broj  , druga mora reći neki broj oblika
, druga mora reći neki broj oblika  pri čemu su
pri čemu su  i
i  prirodni brojevi za koje vrijedi
prirodni brojevi za koje vrijedi 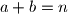 . Igra se zatim nastavlja na isti način, od upravo izrečenog broja. S kojim je sve brojevima mogla započeti igra ako je nakon određenog vremena jedna od njih rekla broj
. Igra se zatim nastavlja na isti način, od upravo izrečenog broja. S kojim je sve brojevima mogla započeti igra ako je nakon određenog vremena jedna od njih rekla broj 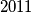 ?
?
 , druga mora reći neki broj oblika
, druga mora reći neki broj oblika  pri čemu su
pri čemu su  i
i  prirodni brojevi za koje vrijedi
prirodni brojevi za koje vrijedi 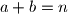 . Igra se zatim nastavlja na isti način, od upravo izrečenog broja. S kojim je sve brojevima mogla započeti igra ako je nakon određenog vremena jedna od njih rekla broj
. Igra se zatim nastavlja na isti način, od upravo izrečenog broja. S kojim je sve brojevima mogla započeti igra ako je nakon određenog vremena jedna od njih rekla broj 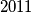 ?
?  Školjka
Školjka 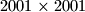 . Igrač može staviti pješaka na prazno mjesto na ploči ako i samo ako u pripadnom retku i stupcu zajedno, ima više od
. Igrač može staviti pješaka na prazno mjesto na ploči ako i samo ako u pripadnom retku i stupcu zajedno, ima više od 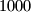 slobodnih mjesta. Gubi onaj igrač koji ne može staviti pješaka. Koji igrač ima pobjedničku strategiju?
slobodnih mjesta. Gubi onaj igrač koji ne može staviti pješaka. Koji igrač ima pobjedničku strategiju? 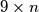 može prekriti pločicama oblika
može prekriti pločicama oblika  tako da se one međusobno ne preklapaju?
tako da se one međusobno ne preklapaju?  ,
,  ,
,  ,
,  u krug tako da zbroj svaka tri uzastopna broja bude najviše:
u krug tako da zbroj svaka tri uzastopna broja bude najviše:


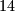
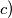

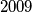 ,
, 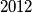 i
i 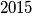 . Željko u svakom koraku označi brojeve na ploči s
. Željko u svakom koraku označi brojeve na ploči s  u nekom poretku, a zatim ih zamjenjuje brojevima
u nekom poretku, a zatim ih zamjenjuje brojevima 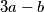 ,
, 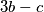 i
i 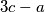 . Može li Željko uzastopnom primjenom ovog postupka postići da na ploči u nekom trenutku pišu tri jednaka broja?
. Može li Željko uzastopnom primjenom ovog postupka postići da na ploči u nekom trenutku pišu tri jednaka broja?