A triangulation of a convex polygon 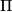 is a partitioning of
is a partitioning of 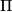 into triangles by diagonals having no common points other than the vertices of the polygon. We say that a triangulation is a Thaiangulation if all triangles in it have the same area.
into triangles by diagonals having no common points other than the vertices of the polygon. We say that a triangulation is a Thaiangulation if all triangles in it have the same area.
Prove that any two different Thaiangulations of a convex polygon 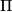 differ by exactly two triangles. (In other words, prove that it is possible to replace one pair of triangles in the first Thaiangulation with a different pair of triangles so as to obtain the second Thaiangulation.)
differ by exactly two triangles. (In other words, prove that it is possible to replace one pair of triangles in the first Thaiangulation with a different pair of triangles so as to obtain the second Thaiangulation.)
A \emph{triangulation} of a convex polygon $\Pi$ is a partitioning of $\Pi$ into triangles by diagonals having no common points other than the vertices of the polygon. We say that a triangulation is a \emph{Thaiangulation} if all triangles in it have the same area.
Prove that any two different Thaiangulations of a convex polygon $\Pi$ differ by exactly two triangles. (In other words, prove that it is possible to replace one pair of triangles in the first Thaiangulation with a different pair of triangles so as to obtain the second Thaiangulation.)
\begin{flushright}\emph{(Bulgaria)}\end{flushright}
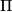 is a partitioning of
is a partitioning of 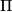 into triangles by diagonals having no common points other than the vertices of the polygon. We say that a triangulation is a Thaiangulation if all triangles in it have the same area.
into triangles by diagonals having no common points other than the vertices of the polygon. We say that a triangulation is a Thaiangulation if all triangles in it have the same area.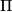 differ by exactly two triangles. (In other words, prove that it is possible to replace one pair of triangles in the first Thaiangulation with a different pair of triangles so as to obtain the second Thaiangulation.)
differ by exactly two triangles. (In other words, prove that it is possible to replace one pair of triangles in the first Thaiangulation with a different pair of triangles so as to obtain the second Thaiangulation.) Školjka
Školjka