Simulacija HMO 2019 zadatak 3 (četvrti dan)
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0Neka je  središte opisane kružnice šiljastokutnog trokuta
središte opisane kružnice šiljastokutnog trokuta  , u kojem vrijedi
, u kojem vrijedi  . Simetrala kuta
. Simetrala kuta  sječe stranicu
sječe stranicu  u točki
u točki  .
.  je polovište dužine
je polovište dužine 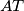 .
.  je točka u unutrašnjosti trokuta
je točka u unutrašnjosti trokuta  takva da je
takva da je 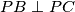 .
. 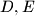 su točke koje leže na okomici iz
su točke koje leže na okomici iz  na
na 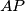 takve da vrijedi
takve da vrijedi 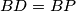 i
i 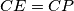 . Ako
. Ako 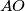 raspolavlja dužinu
raspolavlja dužinu  , dokažite da je
, dokažite da je 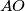 tangenta na opisanu kružnicu trokuta
tangenta na opisanu kružnicu trokuta 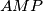 .
.
 Školjka
Školjka 
