Stari Egipćani su površinu četverokuta računali po formuli
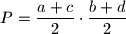
, gdje su

,

,

,

redom duljine stranica

,

,

,
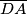
četverokuta

. Dokažite da ta formula daje rezultat koji je veći ili jednak pravoj površini četverokuta. U kojem slučaju je ta formula točna?
%V0
Stari Egipćani su površinu četverokuta računali po formuli $\displaystyle{P=\frac{a+c}{2} \cdot \frac{b+d}{2}}$, gdje su $a$, $b$, $c$, $d$ redom duljine stranica $\overline{AB}$, $\overline{BC}$, $\overline{CD}$, $\overline{DA}$ četverokuta $ABCD$. Dokažite da ta formula daje rezultat koji je veći ili jednak pravoj površini četverokuta. U kojem slučaju je ta formula točna?