Školjka

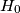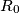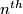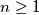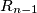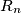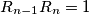A hunter and an invisible rabbit play a game in the Eulidean plane. The hunter's starting point $H_0$ coincides with the rabbit's starting point $R_0$. In the $n^{th}$ th round of the game ($n \geq 1$), the following happens. (1) First the invisible rabbit moves secretly and unobserved from its current point $R_{n-1}$ to some new point $R_n$ with $R_{n-1}R_n = 1$. (2) The hunter has a tracking device (e.g. dog) that returns an approximate position 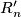$R'_n$ of the rabbit, so that 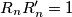$R_nR'_n = 1$. (3) The hunter then visibly moves from point 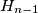$H_{n-1}$ to a new point 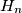$H_n$ with $H_{n-1}H_n = 1$. 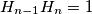Is there a strategy for the hunter that guarantees that after 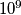$10^9$ such rounds the distance between the hunter and the rabbit is below 100?