IMO Shortlist 2017 problem C5
Kvaliteta:
Avg: 0,0Težina:
Avg: 8,0A hunter and an invisible rabbit play a game in the Eulidean plane. The hunter's starting point 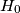 coincides with the rabbit's starting point
coincides with the rabbit's starting point 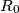 . In the
. In the 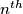 th round of the game (
th round of the game (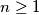 ), the following happens.
), the following happens.
(1) First the invisible rabbit moves secretly and unobserved from its current point 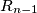 to some new point
to some new point 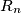 with
with 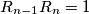 .
.
(2) The hunter has a tracking device (e.g. dog) that returns an approximate position 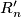 of the rabbit, so that
of the rabbit, so that 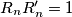 .
.
(3) The hunter then visibly moves from point 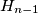 to a new point
to a new point 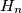 with
with 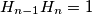 .
.
Is there a strategy for the hunter that guarantees that after 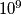 such rounds the distance between the hunter and the rabbit is below 100?
such rounds the distance between the hunter and the rabbit is below 100?
Izvor: https://www.imo-official.org/problems/IMO2017SL.pdf
 Školjka
Školjka 
