Odredite najveći prirodan broj

za koji postoji

-znamenkasti broj

(u dekadskom sustavu) s ovim svojstvima:

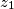
,
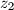
,

,
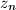
su međusobno različiti brojevi;

za svaki
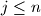
,
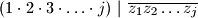
.
Za taj

nađite sve

-znamenkaste brojeve s traženim svojstvima.
%V0
Odredite najveći prirodan broj $n$ za koji postoji $n$-znamenkasti broj $\overline{z_1z_2\ldots z_n}$ (u dekadskom sustavu) s ovim svojstvima:
$(a)$ $z_1$, $z_2$, $\dots$, $z_n$ su međusobno različiti brojevi;
$(b)$ za svaki $j \le n$, $(1\cdot 2\cdot 3\cdot \ldots \cdot j)~|~\overline{z_1z_2\ldots z_j}$.
Za taj $n$ nađite sve $n$-znamenkaste brojeve s traženim svojstvima.