Dan je šiljastokutan trokut  u kojem vrijedi
u kojem vrijedi 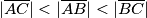 . Neka je
. Neka je  njegova opisana kružnica. Neka je
njegova opisana kružnica. Neka je  točka na
točka na  , na manjem luku
, na manjem luku 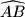 , takva da vrijedi
, takva da vrijedi 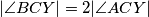 . Neka je
. Neka je  točka na stranici
točka na stranici  takva da vrijedi
takva da vrijedi 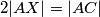 . Neka je
. Neka je  točka osnosimetrična polovištu dužine
točka osnosimetrična polovištu dužine  s obzirom na pravac
s obzirom na pravac  . Dokaži da kružnica opisana trokutu
. Dokaži da kružnica opisana trokutu 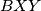 prolazi kroz
prolazi kroz  ako i samo ako joj je središte na
ako i samo ako joj je središte na  .
.
(Ivan Novak)
 Školjka
Školjka