Neka je
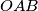
četvrtina kruga sa središtem

polumjera

. Nad dužinama
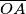
i
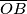
, kao promjerima, konstruirane su polukružnice s unutarnje strane dane četvrtine kruga. Izračunaj polumjer kružnice koja dodiruje te dvije polukružnice i luk

.
%V0
Neka je $OAB$ četvrtina kruga sa središtem $O$ polumjera $1$. Nad dužinama $\overline{OA}$ i $\overline{OB}$, kao promjerima, konstruirane su polukružnice s unutarnje strane dane četvrtine kruga. Izračunaj polumjer kružnice koja dodiruje te dvije polukružnice i luk $AB$.