Učenik je iz jednadžbe
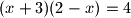
zaključio da je ili
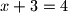
ili
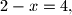
tj. da je

ili
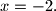
Iako je zaključivanje pogrešno, rješenje je ispravno. Odredite
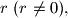
tako da se za dane brojeve

i

istim zaključivanjem iz jednadžbe
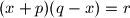
dobije ispravno rješenje.
%V0
Učenik je iz jednadžbe $(x+3)(2-x)=4$ zaključio da je ili $x+3=4$ ili $2-x=4,$ tj. da je $x=1$ ili $x=-2.$ Iako je zaključivanje pogrešno, rješenje je ispravno. Odredite $r\,\,(r \neq 0),$ tako da se za dane brojeve $p$ i $q$ istim zaključivanjem iz jednadžbe $(x+p)(q-x)=r$ dobije ispravno rješenje.