Točka

je središte trokutu

upisane kružnice, a simetrala kuta

siječe stranicu

u točki

. Dokaži da je
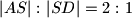
ako i samo ako vrijedi
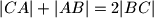
.
%V0
Točka $S$ je središte trokutu $ABC$ upisane kružnice, a simetrala kuta $\angle BAC$ siječe stranicu $\overline{BC}$ u točki $D$. Dokaži da je $|AS|:|SD|=2:1$ ako i samo ako vrijedi $|CA|+|AB|=2|BC|$.