Za
označimo s
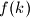
prirodan broj najbliži broju
![\sqrt[4]{k}.](/media/m/5/8/3/5834739b0b947c4112fd372e0e2318b8.png)
Neka je dan
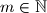
. Koliko ima prirodnih brojeva
za koje je
?
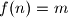
%V0
Za $k \in \mathbb{N}$ označimo s $f(k)$ prirodan broj najbliži broju $\sqrt[4]{k}.$ Neka je dan $m \in \mathbb{N}$. Koliko ima prirodnih brojeva $n$ za koje je $f(n)=m$?
Školjka