Neka su

,

,

pozitivni realni brojevi za koje vrijedi
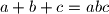
. Dokaži da vrijedi
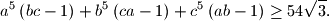
%V0
Neka su $a$, $b$, $c$ pozitivni realni brojevi za koje vrijedi $a+b+c=abc$. Dokaži da vrijedi $$
a^5\left(bc-1\right)+b^5\left(ca-1\right)+c^5\left(ab-1\right)\ge
54\sqrt{3}.
$$