Neka su

i

realni brojevi veći od

takvi da su brojevi
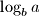
,
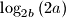
i
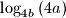
, u tom poretku, uzastopni članovi aritmetičkog niza. Dokaži da su brojevi

i

jednaki.
%V0
Neka su $a$ i $b$ realni brojevi veći od $1$ takvi da su brojevi $\log_b a$, $\log_{2b}{\left(2a\right)}$ i $\log_{4b}{\left(4a\right)}$, u tom poretku, uzastopni članovi aritmetičkog niza. Dokaži da su brojevi $a$ i $b$ jednaki.