Lema 1: Umnožak faktora je nula ako i samo ako je barem jedan od faktora nula.
PRIMJER 1:
Riješi diofantsku jednadžbu: 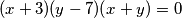 .
.
RJEŠENJE:
Po lemi, vidimo da su rješenja oblika 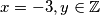 (ako je prva zagrada jednaka nuli),
(ako je prva zagrada jednaka nuli), 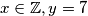 (ako je druga zagrada jednaka nuli) i
(ako je druga zagrada jednaka nuli) i 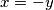 (ako je treća zagrada jednaka nuli; ovo možete zapisati i preko nekog parametra).
(ako je treća zagrada jednaka nuli; ovo možete zapisati i preko nekog parametra).
Nema veze što se neki skupovi rješenja preklapaju, na primjer 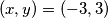 (kada su prva i treća zagrade jednake nuli), bitno je samo da pokrijete sva rješenja.
(kada su prva i treća zagrade jednake nuli), bitno je samo da pokrijete sva rješenja.
PRIMJER 2:
Riješimo diofantsku jednadžbu 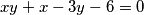 .
.
RJEŠENJE:
Zadana jednadžba zapravo je jednaka: 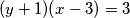 . Dakle, dovoljno je riješiti samo slučajeve kada je jedna zagrada jednaka
. Dakle, dovoljno je riješiti samo slučajeve kada je jedna zagrada jednaka 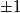 , a druga
, a druga 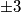 . Sada izjednačavamo zagrade s tim vrijednostima. Konkretno, rješenja su
. Sada izjednačavamo zagrade s tim vrijednostima. Konkretno, rješenja su 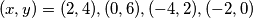 .
.
Zadatci za samostalno rješavanje
1. Riješi u cijelim brojevima: 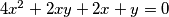 .
.
2. Riješi u cijelim brojevima: 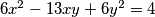 .
.
3. Nađi sva cijelobrojna rješenja za: 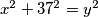 .
.
\textbf{Lema 1:} Umnožak faktora je nula \textit{ako i samo ako} je \textbf{barem} jedan od faktora nula.
PRIMJER 1:
Riješi diofantsku jednadžbu: $(x+3)(y-7)(x+y)=0$.
RJEŠENJE:
Po lemi, vidimo da su rješenja oblika $x=-3, y \in \mathbb{Z}$ (ako je prva zagrada jednaka nuli), $x \in \mathbb{Z}, y=7$ (ako je druga zagrada jednaka nuli) i $x = -y$ (ako je treća zagrada jednaka nuli; ovo možete zapisati i preko nekog parametra).
Nema veze što se neki skupovi rješenja preklapaju, na primjer $(x, y) = (-3, 3)$ (kada su prva i treća zagrade jednake nuli), bitno je samo da pokrijete sva rješenja.
PRIMJER 2:
Riješimo diofantsku jednadžbu $xy + x - 3y - 6 = 0$.
RJEŠENJE:
Zadana jednadžba zapravo je jednaka: $(y + 1)(x - 3) = 3$. Dakle, dovoljno je riješiti samo slučajeve kada je jedna zagrada jednaka $\pm 1$, a druga $\pm 3$. Sada izjednačavamo zagrade s tim vrijednostima. Konkretno, rješenja su $(x, y) = (2, 4), (0, 6), (-4, 2), (-2, 0)$.
\textbf{Zadatci za samostalno rješavanje}
1. Riješi u cijelim brojevima: $4x^2 + 2xy + 2x + y = 0$.
2. Riješi u cijelim brojevima: $6x^2 - 13xy + 6y^2 = 4$.
3. Nađi sva cijelobrojna rješenja za: $x^2 + 37^2 = y^2$.
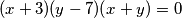 .
.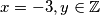 (ako je prva zagrada jednaka nuli),
(ako je prva zagrada jednaka nuli), 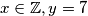 (ako je druga zagrada jednaka nuli) i
(ako je druga zagrada jednaka nuli) i 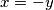 (ako je treća zagrada jednaka nuli; ovo možete zapisati i preko nekog parametra).
(ako je treća zagrada jednaka nuli; ovo možete zapisati i preko nekog parametra).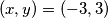 (kada su prva i treća zagrade jednake nuli), bitno je samo da pokrijete sva rješenja.
(kada su prva i treća zagrade jednake nuli), bitno je samo da pokrijete sva rješenja.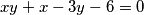 .
.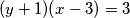 . Dakle, dovoljno je riješiti samo slučajeve kada je jedna zagrada jednaka
. Dakle, dovoljno je riješiti samo slučajeve kada je jedna zagrada jednaka 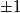 , a druga
, a druga 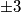 . Sada izjednačavamo zagrade s tim vrijednostima. Konkretno, rješenja su
. Sada izjednačavamo zagrade s tim vrijednostima. Konkretno, rješenja su 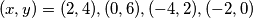 .
.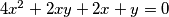 .
.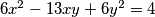 .
.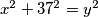 .
.  Školjka
Školjka 
